背景

基于The Impacts of Data, Ordering, and Intrinsic Dimensionality on Recall in Hierarchical Navigable Small Worlds 这篇文章的发现，hnsw 召回的表现和向量的本征维度相关，具体来说，按照向量本征维度，从高到低插入向量，hnsw 召回率比随机好，而如果是按照向量本征维度从低到高插入，hnsw 召回率比随机顺序插入差，整体召回率 gap 最大可达 12%。

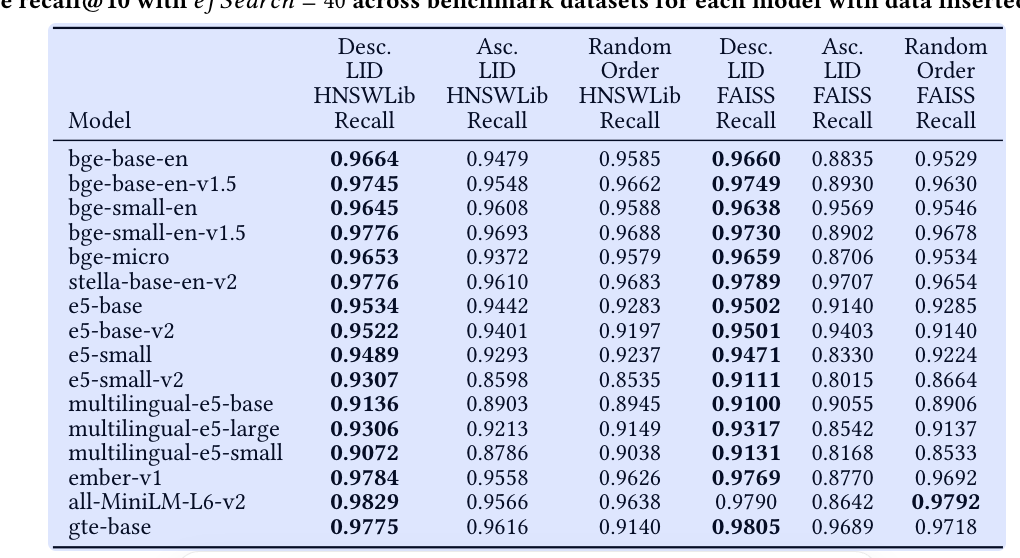
这个数据也测试了，多个 embedding 模型，包括目前广泛使用的 bge 模型，整体召回率表现如下所示：

Desc LID 表示，按照向量内在维度由高到低插入， AscLID 表示按照向量内在维度从低到高，Random 表示随机插入顺序。

内在维度的物理意义

按照维基百科的解释（https://en.wikipedia.org/wiki/Intrinsic_dimension），向量本征维度表示最少用来表示一个数据集的变量个数。可以简单理解为，对于一个向量数据集，向量数据通常在一个低维流形，数据的分布可以用一个子集向量来表示。通俗地说，就是数据实际上分布在多少维的空间里。

示例解释

有时你的数据看起来存储在一个高维空间，比如有100个特征，但其实所有的数据点都只分布在某个二维平面上，这时intrinsic dimension（固有维数）是2，远小于表面的100。
比如一张纸（二维），可以在三维空间中，但其本征维数是2。

详细描述

Intrinsic dimension反映了数据的本质复杂度。
有时候高维数据存在大量冗余，实际可能只与少量变量有关。
常用于降维分析、非线性流形学习（如t-SNE、Isomap）等领域。

数学表达

如果一组数据在nn维空间中，但所有点都在kk维流形（曲面）上，则intrinsic dimension为kk。

Intrinsic dimension（固有维数）在物理上的意义，可以直观理解为一个系统或数据集中，独立自由变化的最小参数数量。就是说，虽然某个物体或现象可能表面上处于高维空间里，但它实际上只“活跃”在一个更低的维度空间内。

物理意义详细解释

自由度的本质数量
在物理学里，“自由度”是描述系统状态所需的独立变量数。Intrinsic dimension描述的是系统最本质、最少的自由度数量。例如：

一个质点在平面上运动，本质自由度是2（横、纵），即intrinsic dimension=2。
一张薄纸虽然在三维空间中，但如果完全平整，没有褶皱、弯曲，本质只需两个坐标（长度和宽度），intrinsic dimension=2。

有效空间“大小”
它告诉我们：尽管数据（或物理对象）处于高维空间，但其分布或结构仅占据一个低维“子空间”。

例如描述气体分子的运动，虽然运动方程在高维空间里，但实际很多状态分布于某种低维流形上。

能量、信息或运动的限制通道
Intrinsic dimension物理上限制了“行为发生”的通道数。比如记录大量温度数据，若所有温度点几乎线性相关，说明信息本质被单一因子控制，intrinsic dimension≈1。

举例

铁丝弯成各种形状放在三维空间，但每个点仅靠一条曲线坐标确定（其实是1维的），intrinsic dimension=1。
手电筒的光斑扫过墙面，最终变化只在2维墙面上，intrinsic dimension=2。
动力学系统：如果一个复杂运动被两个参数完全描述，则系统intrinsic dimension就是2，无论系统嵌入到多高维空间。

总结一句话

Intrinsic dimension的物理意义：
它表示一个物理系统本质可独立变化的参数/自由度的最小数量，揭示了系统本身真正“活跃”的维度，与其表面上的维度无关。

本征维度的计算方案

本征维度（intrinsic dimension）的计算方式有很多种，具体方法会根据数据的类型和研究领域不同而采用不同的技术。以下是常见的几种计算方式简介：

1. 主成分分析（PCA）法

思路：

用PCA将高维数据投影到低维空间，统计可以解释“绝大部分方差”的主成分数目。
通常选取累计方差达到比如95%的主成分个数，作为本征维度的估计。

步骤：

对数据矩阵做中心化。
计算协方差矩阵，做特征值分解。
选主成分数量，使累计贡献率过某一阈值。

适用：数据结构接近线性流形，有较强相关性。

2. 最近邻方法（Nearest Neighbor）

方法举例：Maximum Likelihood Estimation of Intrinsic Dimension (MLE-ID)

思想：
分析点的最近邻距离分布，利用统计特性估算维度。

通用公式（Levina & Bickel, 2005）：

对于每个样本点$x_i$，找其最近的$k$个邻居，记第$j$个邻居的距离为$r_j(x_i)$，则
$$
\hat{d}i = \left[ \frac{1}{k-1} \sum{j=1}^{k-1} \ln \frac{r_k(x_i)}{r_j(x_i)} \right]^{-1}
$$
取所有点的平均，得到最终本征维度估计。

适用：非线性流形，应用很广。

3. 相关维数（Correlation Dimension）

方法：
统计样本点之间的两两距离分布，分析随距离阈值变化，点对增多的规律。

公式：
$$
C(r) = \frac{2}{N(N-1)} \sum_{i<j} I(|\mathbf{x}i-\mathbf{x}_j| < r) $$ 估算相关维数$d$为： $$ d = \lim{r \to 0} \frac{\log C(r)}{\log r}
$$

适用：混沌吸引子、时间序列等场景。

4. 局部线性嵌入/流形学习（LLE/Isomap等）估算

思想：
通过数据嵌入低维流形后，寻找保持局部结构损失最小的维度，为本征维度。

应用：在算法内部选维度参数，也可用重构误差等指标辅助判定。

总结流程（常见实践）

可视化高维数据（PCA前两主成分，是否聚集在低维曲面）
用PCA先粗略估算
用最近邻、相关维数等方法精细估算
若数据为非线性流形，可结合Isomap、LLE等算法内的重要参数选择。

小结

本征维度没有唯一的算法，主要有：

线性方法（PCA主成分计数）
非线性方法（最近邻统计、相关维数、最近邻MLE等）

实际应用中常会同时参考几种方法，取交集或平均值。

如果你有具体的数据类型/领域，可以补充说明，我可帮你推荐适合的方法。

mle-id

MLE-ID（Maximum Likelihood Estimation of Intrinsic Dimension）方法是一种常用的估算数据本征维度的数理统计技术。它利用样本点的最近邻距离分布，以最大似然的思想，计算数据在高维空间中的实际流形维度。

原理

为什么用最近邻？

在高维空间，如果数据分布于低维流形上，那么每个点周围的点分布密度（以及距离的变化规律）与本征维度有关。MLE-ID通过统计点的最近邻距离，对样本点之间的相对位置进行建模，从而估算本征维度。

计算步骤

假设有 $N$ 个数据点，每个点 $\mathbf{x}_i$，在其周围查找 $k$ 个最近邻（$k$一般在3~20之间）。

对于每个点 $\mathbf{x}_i$：

计算其 $k$ 个最近邻的距离：$r_1(\mathbf{x}_i), r_2(\mathbf{x}_i), …, r_k(\mathbf{x}_i)$（升序排列）。
计算如下公式（Levina & Bickel, 2005）： $$
\hat{d}i = \left[ \frac{1}{k – 1} \sum{j=1}^{k-1} \ln \frac{r_k(\mathbf{x}_i)}{r_j(\mathbf{x}_i)} \right]^{-1}
$$
对所有样本点求均值： $$
\hat{d} = \frac{1}{N} \sum_{i=1}^{N} \hat{d}_i
$$

$\hat{d}$ 即为对本征维度的估算结果。

方法特点

无监督，无需标签。
可用于线性/非线性流形上的数据。
对噪声有一定鲁棒性，$k$的选取影响结果细节。
适合大样本，特别常用于流形学习、混沌吸引子等实际数据分析中。

Python 伪代码

import numpy as np
from sklearn.neighbors import NearestNeighbors

def mle_id(X, k=10):
    N = X.shape[0]
    # 寻找最近邻距离
    nbrs = NearestNeighbors(n_neighbors=k+1).fit(X)
    distances, _ = nbrs.kneighbors(X)  # 包括自己，首个距离为0
    distances = distances[:, 1:]  # 去掉自身的距离（为0）
    # 按公式计算每个点的ID
    logs = np.log(distances[:, -1][:, np.newaxis] / distances[:, :-1])
    id_estimates = 1 / np.mean(logs, axis=1)
    return np.mean(id_estimates)

参考文献

Levina, E., & Bickel, P. J. (2005). Maximum likelihood estimation of intrinsic dimension. In NIPS.

总结：
MLE-ID算法通过分析样本最近邻之间的距离结构，以最大似然的方式估算高维数据的本征维度，非常适合用于高维数据流形结构的分析和理解。

本征维度对 ann 检索的影响

你的问题是：本征维度对近似最近邻（Approximate Nearest Neighbor, ANN）检索的影响？

答案如下：

1. 本征维度与检索性能的关系

本征维度是数据实际分布的自由度个数，体现了数据空间的“有效复杂度”。
在ANN场景，如果数据点虽然在高维空间（比如512维、2048维），但实际上本征维度很低，数据都集中分布在一个低维流形上（如10维），这就影响了算法选择和性能表现。

2. 影响具体体现在哪里？

① 查找效率

本征维度低，点之间的几何关系“更有序”易于区分，“最近邻”更直观。很多ANN算法（如树结构、哈希结构等）能有效索引和剪枝。
本征维度高，即使数据维度不是特别高，但本征维度高时，“最近邻”易出现距离收敛、“最近邻现象”变弱，数据分布接近全局平均，“谁都差不多近”，ANN算法效果和效率都会明显下降、易退化。

② 精度表现

低本征维度→高检索精度：恰当算法能精准定位最近邻。
高本征维度→精度下降：距离分布趋同，误检概率升高。

③ 算法选择

若本征维度低，可以用PCA预降维、再用KD树、BallTree等结构。
本征维度高时，传统空间索引（KD树、球树等）几乎“无效”，需考虑基于哈希（LSH）、产品量化（PQ）、图查找（如HNSW）等专门面向高维检索的算法。

④ 存储与硬件资源

数据实际分布低维，ANN存储索引往往可压缩生命周期、减少计算量。
实际本征维度高，数据稀疏、内存消耗大，索引难以压缩。

⑤ “维度灾难”与本征维度

维度灾难实际本质很多时候是本征维度高而不是表面空间维度高。

3. 实践建议

在ANN应用前，建议估算本征维度：
若明显低，可以用PCA/LLE等降维手段；
算法选型可倾向空间索引、聚类等；
本征维度高则用“显式高维算法”，比如HNSW、PQ、IVF等。
实际ANN库（FAISS、Annoy、HNSW等）多已考虑本征维度问题，但降维预处理常常能带来质的提升。

总结

本征维度直接影响ANN索引结构的效率、精度和存储开销，实际数据本征维度越低，算法表现越优。若本征维度高，会面临“维度灾难”，需要专门面向高维流形的索引策略。

如果你有特定的ANN算法或数据类型需求，也可以进一步说明，得到更针对性的建议！

为什么按照本征维度从高到底插入有助于提升 hnsw召回率

这是一个很好也很细致的问题，涉及到数据分布结构、本征维度与HNSW（Hierarchical Navigable Small World）近似最近邻算法的内部机制之间的关系。

我们先分两步解释：

1. HNSW 的原理简述

HNSW 构建了一个多层的“小世界”图，用来索引和搜索向量。
插入点时，会按照一定策略选择“邻居”，并将新点连入这些节点的邻接表。
多层结构自顶向下分配层级，层高与点的随机数相关。
图结构如何连边，与向量之间的距离结构紧密相关。

2. 按照本征维度排序插入的影响

① 本征维度越高，数据的“有效复杂度”越大

本征维度高的数据，点分布更稀疏，空间结构复杂、节点之间差异更大；
本征维度低的数据，点“更集中”更好覆盖，局部结构清晰。

② HNSW插入时的“连边覆盖”性质

先插入高本征维度（复杂、分布分散性强）的向量，这些点由于彼此距离大，容易形成核心“枢纽”或“骨干”节点。
后插入低本征维度（易覆盖、分布密集）的向量，这些点很有可能与前面的“高本征维度点”建立更多连边，改善整个图的连通性（小世界性、导航能力），使检索流程更顺畅。

③ 为什么召回率会变好？

全局导航结构先搭建：
高本征维度数据通常是“全局结构的主干”，其先插入时，HNSW的顶层图会被“支撑”得更好，主干节点分布合理，后续插入补充细节。
低维流形点互联易补全：
低本征维度数据更容易被当前已有结构“覆盖兴趣”，容易补全细致局部，从而整体结构更加均衡，减少死角，提高检索的覆盖率和精准度。
避免早期结构稀缺导致死区：
若先插入低本征维度数据，早期结构可能在“密集流形“里建立，后来的稀疏高本征维度点插入时，难以获得良好覆盖和连边，导致图结构局部死掉，检索时导航到这些区域精准度和覆盖率降低。
近似最近邻搜索的路径优化：
HNSW搜索依赖图的导航路径，先有全局分散支撑节点，后用密集点细化，搜索路径更短、更覆盖关键空间，召回率提升！

3. 结论与建议

插入顺序影响HNSW图的多层结构和连通性。高本征维度→低本征维度的插入顺序，有效提升召回率和导航能力。
这本质上是数据分布特性在算法结构搭建过程中的“自适应”利用——优先用复杂全局骨干节点、后用密集细节补充，达到最优覆盖。

参考/补充

HNSW原论文和社区讨论中也有提及插入顺序对结构和性能有显著影响。本征维度作为全局复杂度的衡量，合理排序就是利用这个分布特性来优化图。
更细节的讨论可以参考：
Yu A, Liu W, et al., “An Efficient and Accurate Approximate Nearest Neighbor Search with Navigable Small World Graphs”, TPAMI
HNSW算法作者 Yury Malkov 在论坛上的回答

总结

先插入本征维度高的点，后插入本征维度低的点，可以让HNSW的图结构更优化，导航更高效，因此召回率会变好。其核心原因是这样可以先构建好全局主干，再细化局部覆盖，减少死角，提升检索路径和覆盖率。

如需更具体案例或代码示例，可再次补充说明！

浏览量: 6

什么是向量的本征维度（intrinsic dimensionality）

背景